During summers, while working at Ninewells Hospital, which is the largest research hospital in the United Kingdom, we made a sonic screwdriver. ...It beams out enough ultrasound to pick up a 4-inch diameter, half-inch thick rubber disk and spin it around (and we can switch the direction of rotation and the rate of spinning). Other members of the team have begun work to raise the operating frequency by two orders of magnitude, which shrinks everything in size, miniaturizing the device. — And by using resonators the power requirements also shrink.

Why? Well, on the one hand, the combination of Magnetic Resonance Imaging with focused ultrasound clearly had further potential for medical treatment, but needed further development, which we contributed to. On a more academic level, our results validated, for the first time directly, something quite general: the theoretically predicted ratio of the orbital angular momentum to linear momentum in a propagating beam.

There were also some other interesting predictions about these sorts of beams (e.g., negative radiation pressure in higher-order Bessel Beams) that we were able to confirm and clarify. Also, our beams serve as rapid, sensitive tests of system aberrations (wibbly wobbly beamy-weamy stuff that we like to have control over).

Moreover, this work provides a model system that fits nicely into teaching, where I have to work hard to convince students that there really isn't anything "orbiting" in the stationary states that we find in solving the Schrödinger equation for the hydrogen atom, even though those states can have orbital angular momentum.

What does orbital angular momentum mean, when nothing is orbiting?

At a soccer stadium, a beach ball might be sent around the stadium by fans “doing the wave” but if you’re a fan, you generally would bat the ball laterally, in order to transfer momentum in that direction: that’s cheating! If, instead, you start with a fan with a stationary ball overhead and the fan simply moves up and down, then you have to ask where does the transverse momentum come from.

By making analogous states with acoustic waves, these ideas become clearer. For example, beneath the blue hockey puck that we acoustically levitate in the video, is an array of one thousand piezoelectric actuators, each simply moving up and down. Surprisingly, this transfers angular momentum if we tailor the phase shift between adjacent actuators.

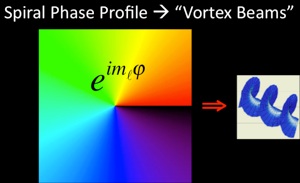
In the left-hand figure above, color represents the relative phase lags we impose on our array of actuators, as we move around a circle. Note that since phase is a periodic variable (ranging from zero to 360°), the horizontal line is not a discontinuity. It's the helicity of the resulting wavefront (shown at right) that allows these waves to transfer angular momentum. Our work looks specifically at the ratio of the orbital angular momentum to the linear momentum carried by a propagating beam, as we move increase the “pitch” of these helical waves (which, again, is a result of the phase profile we impose upon our array of actuators). Importantly, the same “phase factor” describes the stationary states of hydrogen that carry “orbital” angular momentum. It also describes laser modes that carry “orbital” angular momentum.

By the way, one of the (several) advantages of doing this with acoustic waves rather than light waves is that acoustic waves aren't polarized, and this eliminates one source of confusion that may arise in the optical case. — In thinking about optics, most people associate the angular momentum of light with circular polarization, which is really something else entirely: that sort of angular momentum comes from a rotating polarization (and is called "spin" angular momentum or "intrinsic" angular momentum). What we are interested in, instead, is orbital angular momentum, which is (quite generally) associated with helicity of the wavefront.

See:

"The sonic screwdriver," G. C. Spalding, C. Démoré, A. Volovick, Z. Yang, Y. Hertzberg, M. MacDonald, A. Cochran, Proceedings SPIE 8097, 8097-58 (2011).

"Mechanical evidence of the orbital angular momentum to energy ratio of vortex beams," C. Démoré, Z. Yang, A. Volovick, S. Cochran, M. MacDonald, G. C. Spalding, Physical Review Letters 108, 194301 (2012).

Also:

Gabe Spalding & Kishan Dholakia teach a related short course for professionals, to enable you to:

1. •assess a variety of approaches to beam shaping and wavefront correction
   

2. •explain simple protocols for optimizing some beam types of broad interest
   

3. •describe various aspects of data analysis for some wavefront correction algorithms
   

4. •identify key options for enhanced degrees of beam control, resolution, and sensitivity